斐波那契数列(Fibonacci sequence),又称黄金分割数列。数学家莱昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为”兔子数列”,递归出公式如下:
F(0)= 0
F(1)= 1
F(n)= F(n-1) + F(n-2)(n ≥ 2,n ∈ N*)
递归得到的结果为: 1、2、3、5、8、13、21、34、55、89、144、233…
斐波那契数列有如下的特别规律:
1、这个数列从第3项开始,每一项都等于前两项之和。
2、一个完全是自然数的数列,通项公式却是用无理数来表达的。
3、当 n 趋向于无穷大时,前一项与后一项的比值越来越逼近黄金分割0.618,后一项与前一项的比值小数部分越来越逼近 0.618。
4、大自然里存在大量这个数列的动植物特征。
波浪的数学结构
艾略特在他最后的统一结论中解释道,各种波浪的前进有着相同的数学基础,即斐波那契数列主宰着在总体股票指数运动中形成的波浪数。
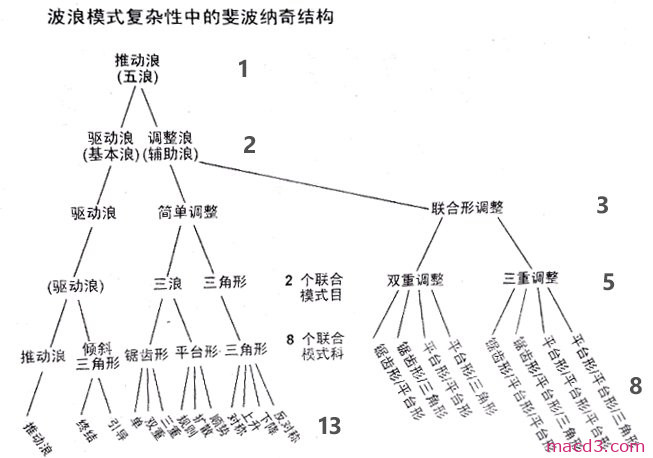
波浪由最小单元组成即推动浪与调整浪,一个调整浪的最简单表现形式是直线下降。一个推动浪的最简单表现是直线上升。一个完整的循环是两条直线。在下一级的复杂形态中,波浪理论的推动浪,浪形为5,调整浪的浪型为3,完整即为8。若把波浪细化,大的推动浪又可分为1、3、5浪为推动,2、4为调整。a、c为推动,b为调整。这样大的推动浪为5+3+5+3+5=21,调整浪为5+3+5=13,合起来为34。如上图,这个数列可以无穷无尽。波浪产生斐波那契数列的事实揭示出,人类总体表达出的情绪锁定在了这条自然的数学法则上。
周期的黄金分割率
由斐波那契数列产生的数字,每两个相连数字相加等于其后第一个数字;前一个数字大约是后一个数字的0.618倍;前一个数字约是其后第二个数字的0.382倍;后一个数字约是前一个数字的1.618倍;后一个数字约是前面第二个数字的2.618倍;
运用到波浪的时间周期上,未来市场转折点=已知时间周期×分割比率。
波浪理论结构的数学关系
甚至波浪理论形态有序的结构复杂性也反映了斐波拉契数列。
1种基本结构 -> 划分为2种波浪 -> 3个简单模式 -> 5种复杂模式(3个推动模式,2个调整模式) -> 13种复杂模式细分型(5推动模式细分型加8个调整模式细分型)。